| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- js
- 파이썬
- Ethereum
- 암호화폐
- 개발
- node js
- 이더리움
- 블록체인개발
- 마스터링 이더리움
- Redis
- keras
- 레디스
- 문자열
- javascript
- 스마트컨트랙트
- 마스터링 비트코인
- 솔리디티
- DAPP
- pythonic
- python
- 마스터링비트코인
- 비트코인
- 알고리즘
- solidity
- smart contract
- 공개키
- 주소
- 개인키
- 백서
- 블록체인
- Today
- Total
개발이야기
[Algorithm] 이론 1 - Interval Scheduling 본문
예제 문제
한 영화배우는 여러 영화 스케줄이 쇄도하는 인기배우다. 이 배우는 최대한 많은 영화를 찍고 싶다.
여러 영화를 한번에 찍을 수 없으며 오직 한 영화만 찍어야한다. 즉, 어떤 영화를 찍고 있다면 다른 영화를
찍으면 안된다. 각 영화의 촬영기간은 다르다.
Solution 1) 가장 빨리 시작하는 영화를 고르기
=> 최대갯수를 선택할 수 없다. 예를 들어 한 영화가 가장 먼저 시작해 가장 나중에 끝나더라도
이 알고리즘에서는 한 영화 밖에 선택할 수 없다. 따라서 이 알고리즘은 정확성이 없으므로
알고리즘이라 할 수 없다.
Solution 2) 작업시간이 가장 짧은 것 고르기
=> 이 해결책이 항상 정확성을 보장할까? 반례가 있다. 영화촬영이 세개 있는데 가장 짧은 작업시간의
영화가 남은 두 영화 사이에 교차해 있다면, 이 해결책은 하나의 영화밖에 고르지 않는다
이 역시 정확성이 없으므로 알고리즘이라 할 수 없다.
Solution 3) 2^n 부분집합
=> 모든 부분집합 중 교차하지 않는것에서 최대 개수를 고른다
=> 정확성은 보장한다. 하지만 시간이 너무 오래걸리는 문제점이 있다.
Solution 4) 가장 빨리 끝나는 작업의 영화 고르기
=> 이 해결책이 항상 옳은 정답을 줄것인가.
(증명) 수학적 귀납법으로 가능하다.
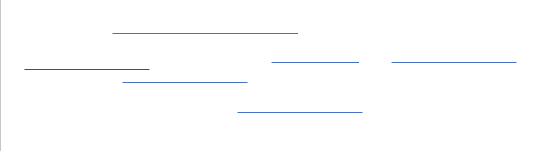
이러한 작업 시간을 가졌을때 빨간색 선이 가장 빨리 작업이 끝나는 영화이다. 이 구간을 구간 E라고 하자
Solution 4에 의하면 구간 E는 가장 빨리 끝나므로 반드시 정답에 포함되어 있어야 한다. 만약 구간E를 포함한
정답이 존재한다면 이 알고리즘의 정당성을 증명할 수 있다.
만약 구간 E를 포함하지 않은 정답 집합이 있다고 해보자.
그 정답 집합에서 가장 빨리 끝나는 구간의 원소는 구간 E보다 작업시간이 늦거나 같다.
만약 그 구간과 구간 E를 교체하여도 정답집합의 다른 원소들과 교차하지 않고 원소의 갯수또한 같다.
따라서 구간 E를 포함한 답이 존재한다.
=> 시간 복잡도 : T(n)
1) 구간 E를 찾는 시간 O(n) : 최악의 경우 모든 원소를 다 봐야하기 때문
2) E와 교차하는 구분선 제거 하는 시간 O(n) : 최악의 경우 모든 원소를 다 봐야하기 때문
T(n) = T(n-1) + O(n) = T(n-1) + n = T(n-2) + (n-1) + n = ... = O(n^2) 의 결과값이 나온다
Solution 5) Solution 4의 최적화 방법
=> 교차하는 부분을 찾는 것을 뒤로 미루는 방법
=> 우선 정답 집합에 넣은 후 앞의 원소와 교차하는 지 비교한다.
=> 시간 복잡도 : T(n)
1) 끝나는 시간을 기준으로 정렬 O(nlogn)
2) 정렬된 원소 끝까지 보며 정답집합 만들기 O(n)
T(n) = O(nlogn) + O(n) 의 결과값이 나온다
Solution 4보다 훨씬 시간이 빨라졌다 !
관련 문제
BOJ 1049 - 기타줄
BOJ 1931 - 회의실 배정
기타 등등 다양한 그리디 알고리즘 문제